ETA Calculation
How a GPS navigation software calculates the ETA
The article explains, how the estimated time of arrival (ETA) is calculated, how it takes live traffic information into account and how we use big data to improve our calculation.
What is the ETA and how is it calculated? The estimated time of arrival is the current time plus the remaining drive time. It is the calculated time when you will most likely arrive at your destination.
In our private lives we see the ETA on the screen of our GPS app. It tells us, when we will arrive at our destination and if we beat it by a couple of minutes it makes us a little proud and we feel good. We use it as a rough indication of the remaining drive time and if it is off by a couple of minutes, it is not a big deal.
Calculate your truck driving time here
Enter Start and Destination — choose with or without Live-traffic and calculate your truck driving time:
This example was implemented using the MapTrip Server-API.
ETA in Transport Planning
In the professional environment however, the ETA is the second most important feature of a GPS navigation software. The most important is obviously to make sure, that the driver reaches his destination. The drive time (or ETA) is the basis for most transport planning tasks. Here, errors in the ETA calculation can accrue to significant dimensions. Precisely predicting the ETA is therefore extremely important.
How the ETA calculation works with traffic information
Let’s look at an example to understand how the ETA is calculated.
A crucial component for the calculation of drive times (and the route itself) is obviously live traffic information. They tell the navigation software how fast traffic is moving currently on a segment. In MapTrip Truck we are using either TomTom or Here for traffic information.
Adding traffic information to the map
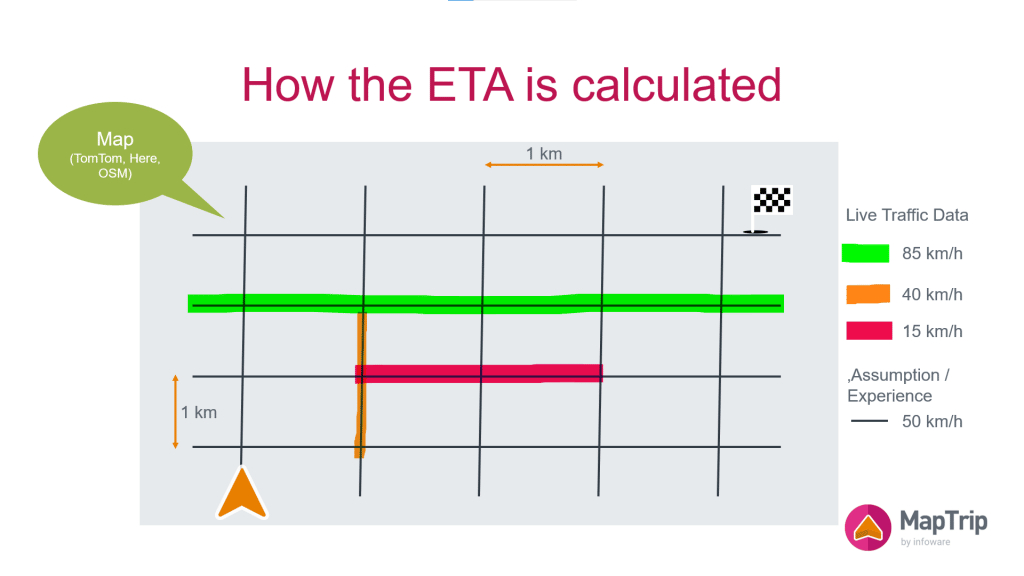
Now we have a map that gives us the distance to the destination and live traffic data which tells us the speed that are currently being driven on those segments. However, the live traffic data is not available for all segments. There are still many grey segments in our sketch which have no live data attributed. In practice these are mostly residential and other minor side roads. The software now assumes speed values for those roads to be able to calculate the time required to traverse those segments. In this example we assume a speed of 50km/h if we have no live traffic data.
Calculating the route
The routing algorithm will now figure out the quickest connection between the current position and the destination.
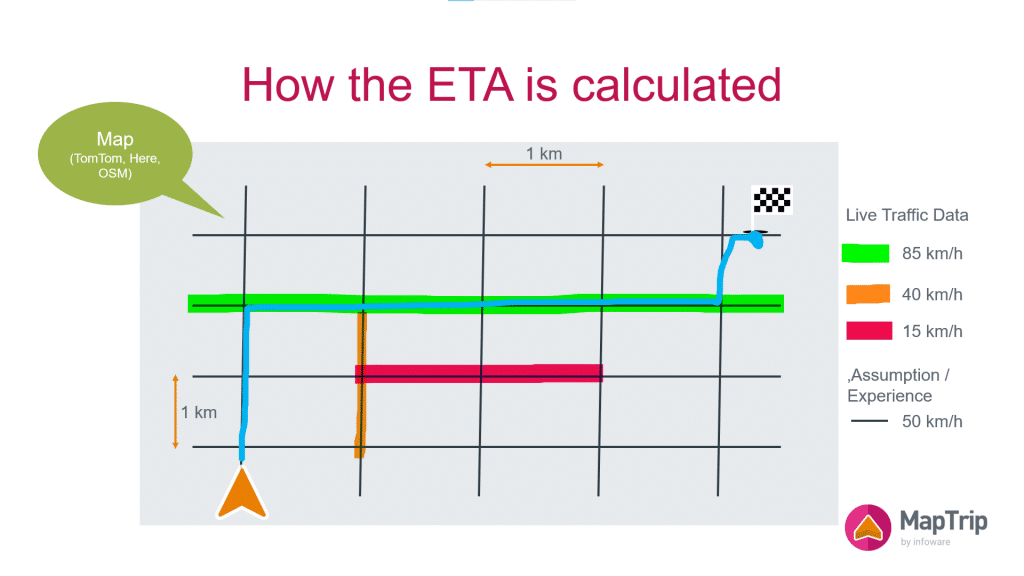
Now that we know the route, it is easy to calculate the drive time.
Calculating the drive time
The route consists of four “green” segments and three “grey” segments. In our sample map each segment has a length of 1km. To calculate the drive time, the length of the segment has to be devided by the speed at which it can be travelled on.
Green: 4km / 85km/h = 0.047h = 2,82min ~ 3min
Grey: 3km / 50km/h = 0.06h = 3.6min
The software will return a total drive time of roughly 6.6min. However, this contains some margin of error.
How to minimize the margin of error in ETA calculation
As we have seen above the drive time calculation and the ETA calculation relies on three types of information:
- the length of the route / of the segments
- the live traffic speeds
- the assumed speeds on segments without traffic
While the length of the route can be assumed to be extremely precise the values of the live traffic and the assumed speeds will inevitably contain some error.
Traffic data are created by averaging the entire traffic on a segment. Speed values from Porsches are averaged with values from trucks and busses. Our typical user drives a truck. Therefore we can ignore speed values over 90km/h. But speed data from traffic is never 100% accurate.
Comparing calculation with measurement
In order to improve our ETA calculation, we found, we need to compare our calculations with actual measurements. As MapTrip is a connected navigation we had the possibility to create a test fleet which sends home the calculated drive time and the actual measured drive time. Thereby we accumulated a vast amount of data which we then analyzed.
For each guidance we had three values:
- length of route
- calculated drive time tc
- actual measured drive time tm
From the calculated drive time and the measured drive time we calculated the relative error Er for each route.
Er = (tc — tm) / tc * 100 [%]
We then plotted the frequency distribution for different intervalls of route lengths. This is what we got.
Frequency distribution of the error in drive time calculation
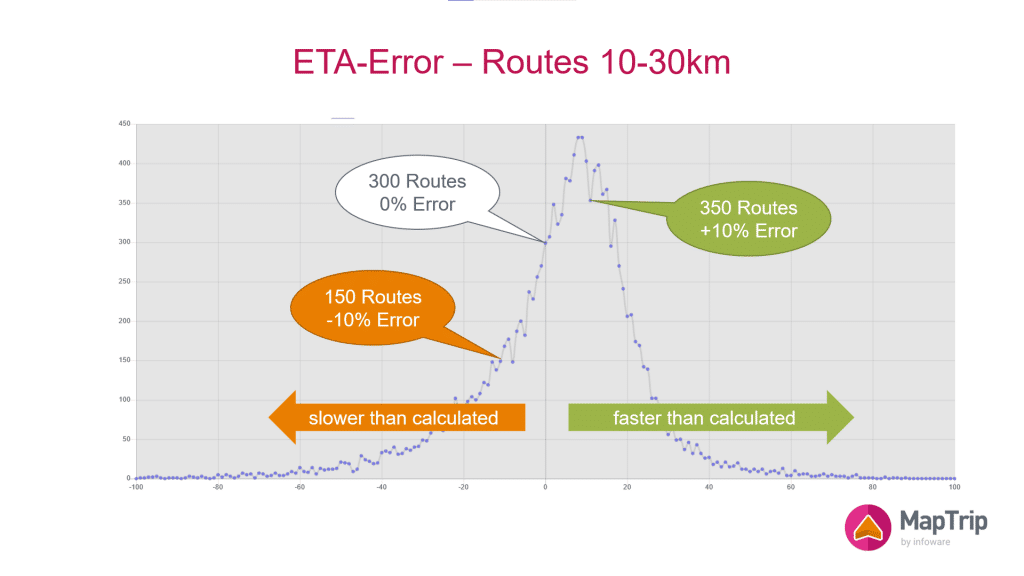
The above graph shows the number of routes with a given relative error Er. The left half of the chart (negative) represents routes where the driver has arrived at the destination later than calculated. The right half of the chart (positive) represents routes where the driver has arrived at the destination later than calculated.
The bubbles point out data points where the error is zero (white), ‑10% (orange) and +10% (green).
The influence of traffic lights on ETA calculation
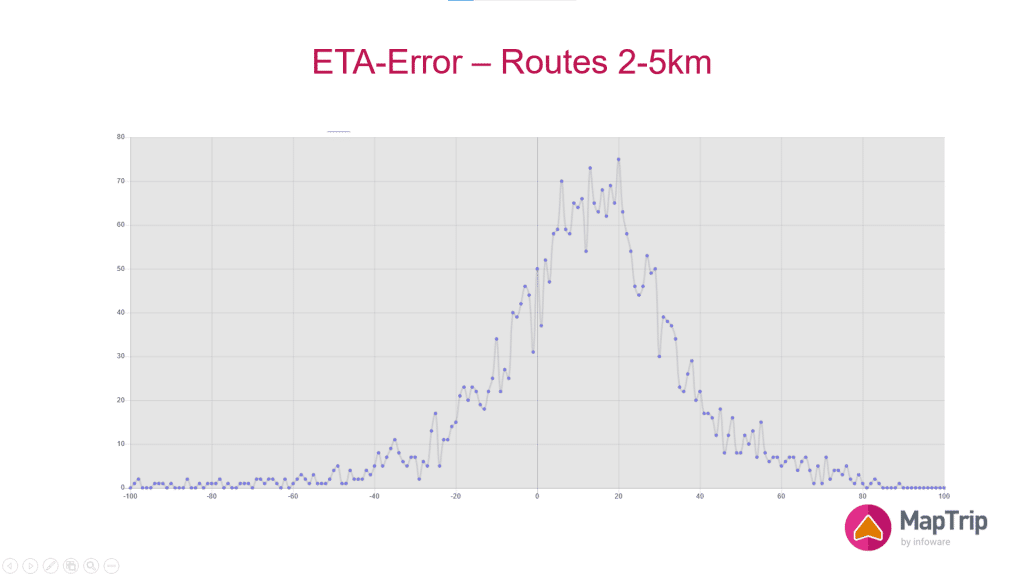
In the above chart you can see the error distribution for routes which are between two and five kilometers long. Please note that the distribution curve is much more evenly spread out to both sides. The curve is much less shaped like a peak but rather like a bell.
The reason for this shape is easy to understand: Imagine a short 2km urban route. If you are unlucky and spend just two minutes waiting in front of a red light, your drive time calculation will already be about 100% off!
Better ETA prediction on long routes
By contrast the ETA prediction becomes more reliable with longer routes.
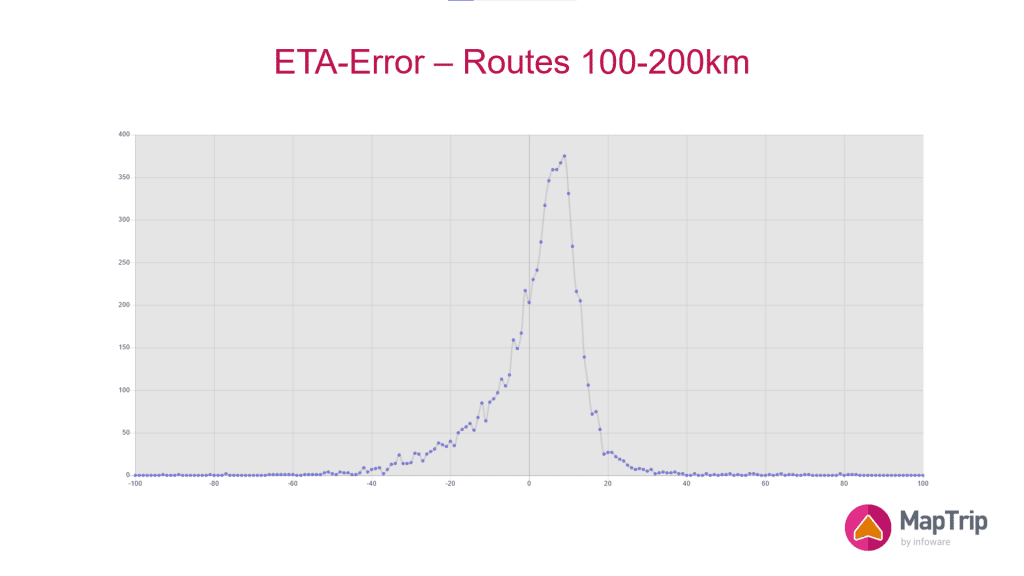
The distribution graph for routes with a length of 100km to 200km has a much more peak-like shape. Please note the sharp drop off after about Er = 10%. This means that hardly anybody beat the ETA by more than that margin (in other words, nobody went faster). This is logical as our test fleet consisted of trucks which have a speed limit of about 90km/h.
On the other side of the peak the distribution is much more spread out. In other words, there were quite a few drivers whos drive time was longer than calculated. This can be explained by unexpected traffic jams (which were not predicted by the traffic information) or, simply, by brake times. Drivers take a break and leave the navigation software in the guidance mode.
Conclusion
The analysis of the actual drive time compared to the calculated drive time is a good means to fine tune the ETA calculation.
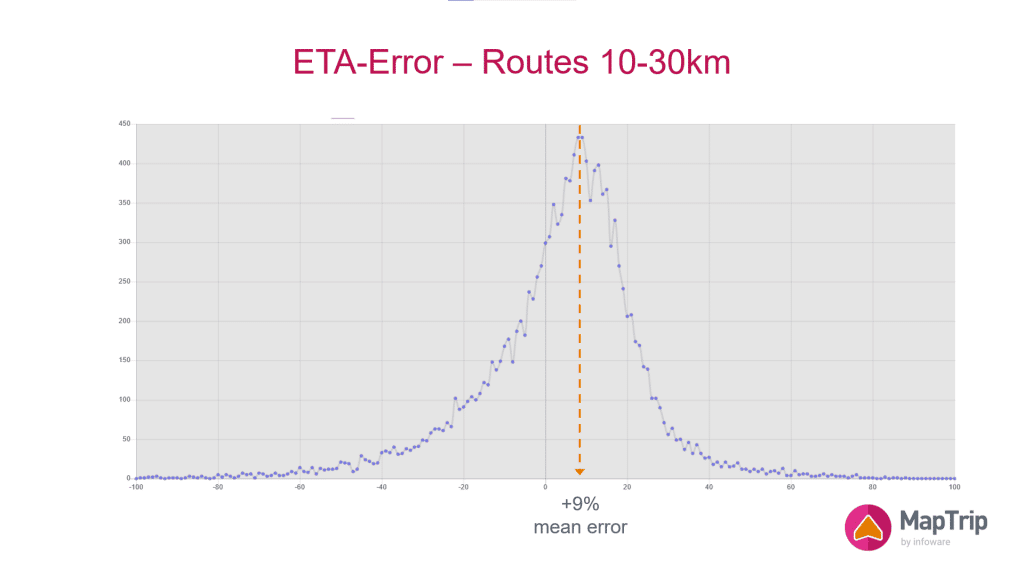
In the shown example the drive time calculation would need a correction of 9% in order to minimize the mean error.
